Login Get started

Bohr's Atomic Model

Manocha Academy・57 minutes read

Niels Bohr proposed the Bohr atomic model where electrons move in fixed orbits around the nucleus, explaining atom stability and line spectra. His postulates included fixed orbits with fixed energy and a quantization condition for angular momentum.

Insights

Niels Bohr proposed the Bohr atomic model, where electrons orbit in fixed paths around the nucleus, addressing the stability of atoms and line spectra observations, unlike previous models.
Bohr's model introduced the concept of quantization of energy levels, explaining how electrons can only accept or release specific amounts of energy during transitions between orbits.
The Bohr model's key postulates include fixed circular orbits with fixed energy for electrons, and the quantization condition that restricts electrons to specific orbits based on their angular momentum, impacting the frequency of radiation absorbed or emitted during transitions.

Get key ideas from YouTube videos. It’s free

Recent questions

What is Bohr's atomic model?
Electrons revolve in fixed orbits around the nucleus.
How is the radius of an electron calculated?
Radius formula is RN = 0.53 n² by Z.
What is the significance of electron excitation?
Excitation moves electrons to higher energy levels.
How does Bohr's model explain energy levels?
Energy levels are quantized and fixed in Bohr's model.
How is the total energy of an electron calculated?
Total energy is the sum of potential and kinetic energies.

Related videos

Summary

00:00

Bohr's Atomic Model Revolutionizes Atomic Theory

Neils Bohr, a famous scientist, challenged Albert Einstein and won the Nobel Prize for his work on the structure of the atom.
Bohr proposed the Bohr atomic model, where electrons revolve in fixed orbits around the nucleus in shells.
Various atomic models were proposed over the years, starting with Dalton's solid sphere model in 1807.
Thompson's Plum pudding model in 1897 suggested electrons embedded in a positive sphere, disproved by Rutherford's nuclear model.
Rutherford's model concentrated positive charge in the nucleus, with electrons orbiting around it.
Bohr's planetary model addressed the drawbacks of Rutherford's model, with electrons in fixed orbits.
Bohr's model explained the stability of atoms and the observation of line spectra, unlike Rutherford's model.
Bohr's postulates included fixed circular orbits with fixed radius and energy for electrons.
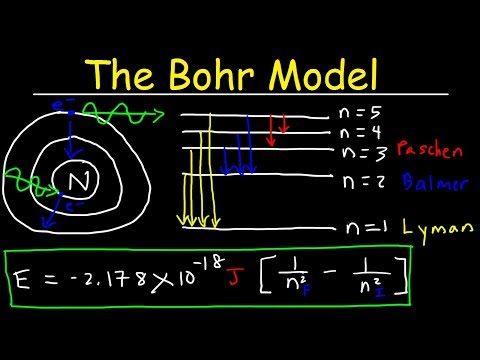
Bohr's quantization condition stated that electrons can only revolve in orbits where angular momentum is NH/2π.
The frequency of radiation absorbed or emitted during electron transitions is determined by the change in energy divided by Planck's constant.

17:45

Atomic Model: Electron Shell Calculation Formula

The n integer represents the shell number in B's model of the atom.
Electrons revolve around the nucleus similar to planets around the Sun in the solar system.
The force between the positively charged nucleus and negatively charged electron is the electrostatic force.
The formula for electrostatic force is 1x4 Pi Epsilon q1 Q2 by r², where q1 and Q2 are charges, and r is the distance between them.
The electrostatic force acts as the centripetal force, pulling the electron towards the nucleus.
The centripetal force formula is MV² by R for a particle in circular motion.
Equating the electrostatic force to the centripetal force leads to the expression 1x4 Pi Epsilon ZD E by r² equals MV² by R.
The final expression for the radius of the electron is RN = 0.53 n² by Z, in angstroms.
The radius of hydrogen's shells can be calculated using the formula RN = 0.53 n² by Z, where n is the shell number and Z is the atomic number.
The model is applicable to hydrogen and single-electron species like H+ ion, not atoms with multiple electrons.

35:26

Electron Shell Formulas and Energy Calculations

The formula to calculate the radius of the electron shell is R = 0.53 * n² / Z, where Z is the atomic number.
This formula is applicable for single electron species like H+ or Li+ by substituting the respective atomic numbers.
To find the velocity of the electron, use the formula V = 2.18 * 10^6 * Z / n m/s in the nth shell.
The kinetic energy of the electron is given by half * m * V², where V is the velocity of the electron.
The kinetic energy formula in the nth shell is derived as 13.6 * Z² / n² electron volts.
The potential energy of the electron is calculated using the formula 1 / (4 * Pi * Epsilon) * q1 * q2 / R, where q1 is the charge of the electron and q2 is the charge of the nucleus.
The potential energy formula in the nth shell is found to be -2 * 13.6 * Z² / n² electron volts.
The total energy of an electron is the sum of its potential and kinetic energies.
The potential energy is negative due to the reference point being at infinity where the energy is considered zero.
The explanation for the negative potential energy is that as the electron moves closer to the nucleus, it releases energy, making its potential energy negative.

52:35

Energy Levels and Electron Behavior in Atoms

The formula for potential energy is -2 * 13.6 * Z² / n², with a negative factor of two, while kinetic energy is 30 * 13.6 * Z² / n², both in electron volts.
Simplifying the formula results in a total energy of -3.6 * Z² / n² electron volts for the N shell of an atom, with negative total energy due to the electron losing energy as it approaches the nucleus.
Applying the total energy formula to the hydrogen atom's electron in different shells reveals the energy levels: -3.6 eV for the first shell, -3.4 eV for the second, -1.51 eV for the third, and -0.85 eV for the fourth shell.
Moving from lower to higher shells increases the electron's energy, as seen in the increasing negative values from shell to shell.
The maximum energy of an electron occurs when it is very far from the nucleus, with a total energy of zero, signifying the electron is free from the atom, turning it into a cation.
Bore's first postulate states electrons in fixed circular orbits have fixed energy, while the third postulate explains how electrons can gain or lose energy when changing orbits.
Excitation occurs when an electron gains energy, moving to higher shells, while de-excitation happens when it loses energy, moving to lower shells.
Electrons require specific amounts of energy to move between energy levels, with the difference in energy levels determining the necessary energy for excitation or de-excitation.
Bore's model couldn't explain the atomic spectrum's line spectrum, where atoms emit specific colors due to electrons only accepting certain energy levels, leading to the emission of light of specific frequencies.
Bore's fourth postulate addresses the quantization of energy levels, where electrons only accept or release specific amounts of energy, explaining the discrete nature of the atomic spectrum.

01:08:58

Calculating Radiation Frequency and Atomic Models

The frequency of radiation absorbed or emitted during electron transitions can be calculated using the formula: frequency (f) equals change in energy (Delta e) divided by Plank's constant (H), where H is 6.626 * 10^-34 J second. This formula helps determine the frequency of electromagnetic waves emitted or absorbed by dividing the energy difference by Plank's constant. Additionally, the wavelength of radiation can be calculated using the formula: velocity of the wave (c) equals frequency (F) times wavelength (Lambda), explaining the atomic spectrum and the fixed frequency lines observed.
Various atomic models have been proposed over the years, starting with John Dalton's atom model in 1807, followed by JJ Thompson's plum pudding model in 1897, and Ernest Rutherford's nuclear model in 1911. Niels Bohr's planetary model in 1913 addressed the limitations of Rutherford's model, but it also had drawbacks. Subsequently, the Schrödinger quantum model was introduced in 1926, which will be discussed in a separate video.

Try it yourself — It’s free.