Transformation Introduction O levels | Reflection | Rotation | Translation | Enlargement | 4024
Mathswithmurad・52 minutes read
Transformation includes isometric and non-isometric types, with examples like reflection, rotation, translation, and enlargement explained in detail, including formulas and calculations for each type. Practical examples and techniques for finding coordinates, applying tricks, and determining scale factors are provided, with emphasis on the importance of center positions in different transformations.
Insights
- Isometric transformations, which include reflection, rotation, and translation, involve specific rules such as changing coordinates based on mirror lines and rotation angles. These transformations are crucial in altering the position and orientation of objects in a plane.
- Enlargement, a type of non-isometric transformation, focuses on scaling objects based on a center point and a scale factor. Understanding how to calculate the scale factor and apply it correctly is essential in enlarging objects while maintaining their proportions and relationships with other elements in the plane.
Get key ideas from YouTube videos. It’s free
Recent questions
What are the two types of transformations discussed?
Isometric and non-isometric.
How is reflection defined in transformation?
Flipping an object over a line of reflection.
What is the process of rotation in transformation?
Involves center, angle, and direction.
How is enlargement explained in transformation?
Center of enlargement and scale factor.
What is the significance of matrices in transformations?
Used for reflection, rotation, and enlargement.
Related videos

Khan Academy
Introduction to transformations | Transformations | Geometry | Khan Academy
Khan Academy
Transformations - dilation

Khan Academy
Examples recognizing transformations

GateWay Classes
Lec-3 I Unit-1| Matrices I Engg.Mathematics-1 | B.Tech First Year | by Gulshan sir

Physics Wallah - Alakh Pandey
Rotational Motion - 01 || Torque and Moment Of Inertia || NEET Physics Crash Course
Summary
00:00
Types and Techniques of Geometric Transformation
- Transformation is the topic of discussion in today's class, with two types: isometric and non-isometric.
- Isometric transformation includes reflection, rotation, and translation.
- Non-isometric transformation involves enlargement.
- Reflection involves flipping an object over a line of reflection, with the X and Y axes acting as mirror lines.
- Four basic cases of reflection involve changes in coordinates based on the mirror line.
- Perpendicular bisector of object and image determines the line of reflection.
- Rotation includes center of rotation, angle of rotation, and direction (clockwise or anti-clockwise).
- Coordinates change based on the rotation angle and direction, with examples provided.
- Finding the image after rotation involves swapping coordinates and changing signs.
- When the center of rotation is not at (0,0), subtract the center, apply the trick on Y, and then add the center back.
16:26
Rotating Triangle ABC: Tricks and Techniques
- Triangle ABC E is rotated 90 degrees clockwise.
- A B changes to Bima my A due to the rotation.
- The center is given as negative zero.
- The first coordinate chosen is 3 1 3.
- Applying the trick, the coordinate becomes 1 0.
- The second coordinate is 5 and back, becoming -3 -4.
- After applying the negative four trick, it becomes 4 3.
- 270 degrees anti-clockwise equals 90 degrees clockwise.
- The longer method of rotation without tricks is explained.
- Describing the transformation from A to B involves marking points and drawing perpendicular bisectors.
31:02
Understanding Translation and Enlargement in Matrices
- Translation matrix is explained, focusing on object coordinates and translation values.
- The process of translating objects using matrices is detailed, with examples of coordinates and calculations.
- The concept of marking images after translation is emphasized.
- Enlargement is introduced, highlighting the importance of the center of enlargement and scale factor.
- Instructions for enlarging objects with a given center and scale factor are provided.
- An example of enlarging a triangle with specific coordinates and scale factor is demonstrated.
- The formula for calculating the scale factor in enlargement is explained.
- The significance of positive and negative scale factors in relation to object and image direction is clarified.
- The impact of scale factor values on object size in enlargement is discussed.
- Practical cases and examples are used to illustrate the concepts of enlargement and scale factor calculation.
46:12
Finding Center of Enlargement and Scale Factors
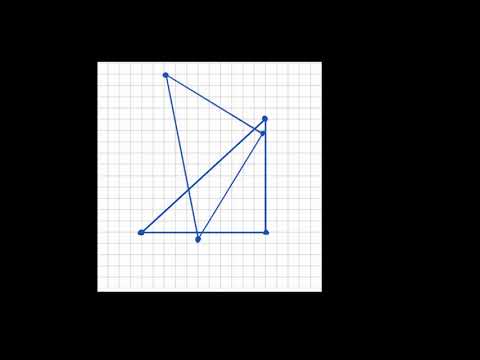
- The method to find the center of enlargement involves connecting all vertices of a triangle with straight lines.
- The intersection point of these lines is identified as the center of enlargement.
- The current center of enlargement is at coordinates 31, 31.
- When determining the scale factor (k), count the number of blocks in the object and image.
- If the object and image move in the same direction, the scale factor is positive; if in opposite directions, it's negative.
- Enlargement is described with the center at 31, 31 and a negative scale factor.
- To calculate the area of the image after enlargement, use the formula: scale factor squared multiplied by the area of the object.
- The formula for the area of similar figures involves the scale factor squared and the ratio of the areas of the object and image.
- Matrices are used for transformations, with specific patterns for reflection, rotation, and enlargement.
- The transformation matrix multiplied by the object yields the image, with different rules for reflection, rotation, and enlargement.




