What is a force in physics?

A force in physics is a vector quantity that has both magnitude and direction, measured in newtons (N). It is a fundamental concept that describes the interaction between objects, causing them to accelerate, decelerate, or change direction. The relationship between force, mass, and acceleration is encapsulated in Newton's second law, which states that the force acting on an object is equal to the mass of that object multiplied by its acceleration (F = m × a). This means that a greater force is required to accelerate a heavier object compared to a lighter one. Understanding forces is crucial for analyzing physical situations and solving problems related to motion and interactions between objects.

How do you calculate gravitational force?

Gravitational force can be calculated using the formula F_g = m × g, where F_g is the gravitational force, m is the mass of the object, and g is the acceleration due to gravity, which is approximately 9.82 m/s² near the Earth's surface. This formula indicates that the weight of an object, or the force of gravity acting on it, increases with its mass. For example, a 1 kg object would experience a gravitational force of about 9.82 N. This concept is essential in understanding how objects behave under the influence of gravity, such as falling or being supported by a surface.

What are Newton's three laws of motion?

Newton's three laws of motion are fundamental principles that describe the relationship between the motion of an object and the forces acting on it. The first law states that an object at rest stays at rest, and an object in motion continues in motion with the same speed and in the same direction unless acted upon by a net external force. The second law establishes that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass (F = m × a). The third law asserts that for every action, there is an equal and opposite reaction, meaning forces always occur in pairs. These laws form the foundation for classical mechanics and are crucial for analyzing the motion of objects.

What is frictional force?

Frictional force is a contact force that opposes the relative motion of two surfaces in contact. It acts in the opposite direction to the movement of an object and is crucial for everyday activities, such as walking or driving. The magnitude of the frictional force can be calculated using the formula F_friction = μ × F_normal, where μ is the coefficient of friction (a measure of how much frictional force exists between two surfaces) and F_normal is the normal force acting on the object, which is perpendicular to the surface. Friction can be beneficial, providing the necessary grip for movement, but it can also be a hindrance, causing wear and energy loss in mechanical systems.

How do you find the resultant force?

The resultant force, or net force, on an object is determined by vectorially adding all the individual forces acting on it. If forces are acting in the same direction, they can be summed directly. If they are acting in opposite directions, the smaller force is subtracted from the larger one. For forces acting at angles, trigonometric functions can be used to resolve them into their x and y components. The overall net force can then be calculated using the Pythagorean theorem to find the magnitude and the inverse tangent function to determine the direction. Understanding the resultant force is essential for predicting how an object will move, as it dictates the object's acceleration according to Newton's second law.

Fysik 1 - Krafter del 1

Räkna med mig! - Börje Sundvall・47 minutes read

Forces are essential in physics as vector quantities that have both magnitude and direction, with various types including contact, gravitational, and frictional forces, all of which are critical for understanding motion and interactions between objects. Newton's laws of motion, which relate force, mass, and acceleration, provide a framework for calculating resultant forces and analyzing situations in both static and dynamic contexts.

Insights

Forces are key to understanding physics, defined as a vector quantity with both magnitude and direction, measured in newtons (N), where 1 newton accelerates a 1 kg mass by 1 m/s². This foundational concept is rooted in Newton's second law, illustrating the relationship between force, mass, and acceleration.
Different types of forces exist, including contact forces like pushing and pulling, and non-contact forces such as gravity and electromagnetic forces. Contact forces require direct interaction, while gravitational and electric forces can influence objects from a distance, showcasing the variety of interactions in physical systems.
Newton's laws of motion provide a framework for analyzing movement: the first law states that objects remain at rest or in uniform motion unless acted upon by a net force; the second law connects force with mass and acceleration; and the third law emphasizes that every action has an equal and opposite reaction, which can be seen in interactions like the gravitational pull between the Earth and the Moon.
The calculation of net forces involves summing all acting forces, with the resultant force determining an object's motion. For example, if multiple forces act on an object in different directions, trigonometric functions can resolve these into components, allowing for a precise calculation of the net force's magnitude and direction.
Practical applications of these concepts can be illustrated through real-world examples, such as a cyclist experiencing a net force while pedaling against air resistance, or a stone falling under the influence of gravity and air resistance. These scenarios demonstrate how forces interact and influence motion, providing insight into everyday physical phenomena.

Get key ideas from YouTube videos. It’s free

Recent questions

What is a force in physics?
A force in physics is a vector quantity that has both magnitude and direction, measured in newtons (N). It is a fundamental concept that describes the interaction between objects, causing them to accelerate, decelerate, or change direction. The relationship between force, mass, and acceleration is encapsulated in Newton's second law, which states that the force acting on an object is equal to the mass of that object multiplied by its acceleration (F = m × a). This means that a greater force is required to accelerate a heavier object compared to a lighter one. Understanding forces is crucial for analyzing physical situations and solving problems related to motion and interactions between objects.
How do you calculate gravitational force?
Gravitational force can be calculated using the formula F_g = m × g, where F_g is the gravitational force, m is the mass of the object, and g is the acceleration due to gravity, which is approximately 9.82 m/s² near the Earth's surface. This formula indicates that the weight of an object, or the force of gravity acting on it, increases with its mass. For example, a 1 kg object would experience a gravitational force of about 9.82 N. This concept is essential in understanding how objects behave under the influence of gravity, such as falling or being supported by a surface.
What are Newton's three laws of motion?
Newton's three laws of motion are fundamental principles that describe the relationship between the motion of an object and the forces acting on it. The first law states that an object at rest stays at rest, and an object in motion continues in motion with the same speed and in the same direction unless acted upon by a net external force. The second law establishes that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass (F = m × a). The third law asserts that for every action, there is an equal and opposite reaction, meaning forces always occur in pairs. These laws form the foundation for classical mechanics and are crucial for analyzing the motion of objects.
What is frictional force?
Frictional force is a contact force that opposes the relative motion of two surfaces in contact. It acts in the opposite direction to the movement of an object and is crucial for everyday activities, such as walking or driving. The magnitude of the frictional force can be calculated using the formula F_friction = μ × F_normal, where μ is the coefficient of friction (a measure of how much frictional force exists between two surfaces) and F_normal is the normal force acting on the object, which is perpendicular to the surface. Friction can be beneficial, providing the necessary grip for movement, but it can also be a hindrance, causing wear and energy loss in mechanical systems.
How do you find the resultant force?
The resultant force, or net force, on an object is determined by vectorially adding all the individual forces acting on it. If forces are acting in the same direction, they can be summed directly. If they are acting in opposite directions, the smaller force is subtracted from the larger one. For forces acting at angles, trigonometric functions can be used to resolve them into their x and y components. The overall net force can then be calculated using the Pythagorean theorem to find the magnitude and the inverse tangent function to determine the direction. Understanding the resultant force is essential for predicting how an object will move, as it dictates the object's acceleration according to Newton's second law.

Summary

00:00

Fundamentals of Forces in Physics

Forces are a fundamental concept in physics, defined as a vector quantity that has both magnitude and direction, and are measured in newtons (N). A force of 1 newton is the force required to accelerate a 1 kg mass by 1 meter per second squared (1 m/s²) in the absence of friction.
The unit of force, the newton, can also be expressed as kilograms times meters per second squared (kg·m/s²), highlighting the relationship between mass, acceleration, and force as described by Newton's second law: F = m × a.
There are various types of forces, including contact forces (e.g., push and pull), gravitational forces (weight), electric forces, magnetic forces, and frictional forces. Contact forces require physical interaction, while gravitational and electric forces can act at a distance.
The force of gravity (F_g) acting on an object can be calculated using the formula F_g = m × g, where g is the acceleration due to gravity, approximately 9.82 m/s² near the Earth's surface. This value can vary slightly based on location.
Newton's law of gravitation states that the force between two masses is calculated using the formula F = G × (m₁ × m₂) / r², where G is the gravitational constant (approximately 6.67 × 10⁻¹¹ N·m²/kg²) and r is the distance between the centers of the two masses.
Frictional force is a contact force that opposes motion and acts in the opposite direction of an object's movement. It can be calculated using the formula F_friction = μ × F_normal, where μ is the coefficient of friction and F_normal is the normal force acting on the object.
The normal force acts perpendicular (90 degrees) to the surface on which an object rests. On a flat surface, it is equal to the weight of the object, but on an inclined surface, it must be calculated based on the angle of inclination.
Newton's three laws of motion are essential for solving physics problems: the first law states that an object at rest stays at rest, and an object in motion stays in motion unless acted upon by a net force; the second law relates force, mass, and acceleration; and the third law states that for every action, there is an equal and opposite reaction.
The resultant force (net force) on an object is the vector sum of all forces acting on it. If the net force is zero, the object is either at rest or moving at a constant speed in a straight line, indicating that all forces are balanced.
Understanding these concepts and calculations is crucial for analyzing physical situations and solving problems related to forces, motion, and interactions between objects in various contexts.

17:17

Understanding Forces and Motion Principles

An object at rest or moving at a constant speed, such as a car driving at 100 km/h with cruise control, experiences a net force of zero, despite various forces acting on it, like air resistance and engine thrust.
For an object to maintain constant speed, it must move in a straight line; if it turns while maintaining speed, it experiences acceleration, indicating a net force is present.
Satellites orbiting Earth travel at a constant speed but are subject to a net force due to gravitational attraction, which continuously alters their direction.
Newton's second law states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass, expressed mathematically as \( a = \frac{F_{net}}{m} \).
The formula can be rearranged to \( F_{net} = m \cdot a \), illustrating that a larger mass results in a smaller acceleration for the same net force applied.
Newton's third law asserts that for every action force, there is an equal and opposite reaction force; forces always occur in pairs acting on different objects.
An example of Newton's third law is the gravitational interaction between the Earth and the Moon, where the Earth exerts a gravitational force on the Moon, and the Moon exerts an equal and opposite force on the Earth.
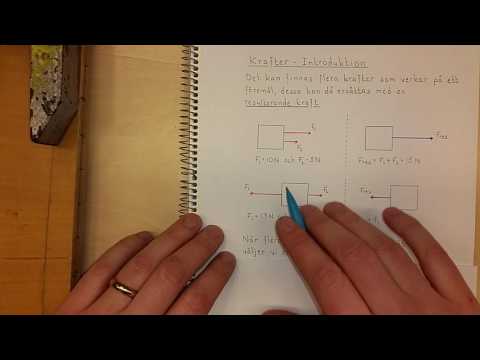
In force diagrams, forces acting on an object can be represented as arrows; for instance, a force of 10 N acting upwards and a force of 20 N acting downwards results in a net force of 10 N downwards.
When forces act in opposite directions, such as 10 N to the left and 10 N to the right, they cancel each other out, resulting in a net force of zero.
For calculating resultant forces from oblique forces, one can use trigonometric functions to resolve forces into their x and y components, applying the Pythagorean theorem to find the magnitude of the resultant force.

33:08

Force Analysis and Calculations in Physics

The discussion begins with analyzing a scenario involving an angle of 30 degrees, where the force components are defined as F2x and F2y, with F2x being the adjacent side and F2y the opposite side in relation to the angle. The cosine function is used to calculate F2x, while the sine function is used for F2y, emphasizing the relationship between the angle and the force components.
To calculate F2x, the formula used is F2x = magnitude of the oblique force × cos(30 degrees), resulting in F2x = 7 cos(30) = approximately 6.06 N. For F2y, the calculation is F2y = magnitude of the oblique force × sin(30 degrees), yielding F2y = 7 sin(30) = 3.5 N.
The net force in the x-direction is determined by adding F2x and another force F1, which is given as 10 N. Thus, the total force in the x-direction is F_net_x = F2x + F1 = 6.06 N + 10 N = 16.06 N.
The net force in the y-direction is solely F2y, which is 3.5 N. The overall net force is calculated using the Pythagorean theorem, resulting in a net force magnitude of F_net = √(F_net_x² + F_net_y²) = √(16.06² + 3.5²) = approximately 16.4 N.
The angle of the net force relative to the positive x-axis is calculated using the tangent function: tan(θ) = opposite/adjacent = F_net_y/F_net_x = 3.5/16.06. The angle θ is found using the inverse tangent function, yielding θ = arctan(3.5/16.06) = approximately 12 degrees.
The net force has a magnitude of 16.4 N and is directed at an angle of 12 degrees north of the positive x-axis, indicating the direction of the resultant force vector.
A practical example is introduced involving a book weighing 0.5 kg on a table, with a coefficient of friction of 0.25. The gravitational force acting on the book is calculated as Fg = mass × g = 0.5 kg × 9.82 m/s² = approximately 4.9 N.
The normal force (FN) acting on the book is equal to the gravitational force, thus FN = 4.9 N. The maximum frictional force is calculated as F_friction_max = coefficient of friction × FN = 0.25 × 4.9 N = approximately 1.225 N.
When applying forces of 0.5 N, 1 N, and 1.5 N laterally to the book, it is determined that the book remains at rest under 0.5 N and 1 N due to friction being able to counteract these forces, while it begins to move when a force of 1.5 N is applied, resulting in a net force of 0.3 N to the right.
Another scenario involves a box with a mass of 5 kg being pulled with a force of 20 N at an angle of 25 degrees. The gravitational force is calculated as Fg = 5 kg × 9.82 m/s² = approximately 49 N. The components of the pulling force are calculated as FX = 20 cos(25) and FY = 20 sin(25), leading to a normal force adjustment based on the vertical forces acting on the box.

51:23

Forces and Acceleration in Motion Scenarios

A cyclist exerts a traction force of 200 N while experiencing an air resistance of 50 N, resulting in a net force of 150 N to the right. Given the combined mass of the cyclist and bicycle is 80 kg, the acceleration can be calculated using the formula \( F_{net} = m \cdot a \), leading to an acceleration of 1.875 m/s² (150 N / 80 kg).
A stone weighing 2 kg falls from a height of 200 m, affected by air resistance that is 10% of the gravitational force. The gravitational force is calculated as \( 2 \, \text{kg} \times 9.81 \, \text{m/s}^2 = 19.62 \, \text{N} \), and the air resistance is \( 0.1 \times 19.62 \, \text{N} = 1.962 \, \text{N} \). The net force acting on the stone is 17.658 N (19.62 N - 1.962 N).
The acceleration of the stone can be determined using \( a = \frac{F_{net}}{m} \), resulting in \( a = \frac{17.658 \, \text{N}}{2 \, \text{kg}} = 8.829 \, \text{m/s}^2 \). To find the time of fall, the formula \( t = \sqrt{\frac{2 \cdot s}{a}} \) is used, where \( s = 200 \, \text{m} \) and \( a = 8.829 \, \text{m/s}^2 \), yielding a fall time of approximately 6.36 seconds.
A car weighing 1 ton (1000 kg) decelerates from 70 km/h to 50 km/h in 3 seconds. The change in speed is calculated as \( 50 - 70 = -20 \, \text{km/h} \), which converts to \( -5.56 \, \text{m/s} \) (by dividing by 3.6). The acceleration is then \( a = \frac{-5.56 \, \text{m/s}}{3 \, \text{s}} = -1.85 \, \text{m/s}^2 \).
The net force acting on the car during braking is calculated using \( F_{net} = m \cdot a \), resulting in \( F_{net} = 1000 \, \text{kg} \times -1.85 \, \text{m/s}^2 = -1850 \, \text{N} \) (or -1.85 kN), indicating that the force acts in the opposite direction of the car's motion.

Fysik 1 - Krafter del 1

Insights

Get key ideas from YouTube videos. It’s free

Recent questions

Related videos

Fysik 1 Krafter - Introduktion

What is a Force & Types of Forces in Physics? - Gravity, Normal Force, Contact Forces - [1-5-1]

GCSE Physics Revision "Contact and Non-contact Forces"

Laws of Motion Class 11 Physics Chapter 4 One Shot | New NCERT CBSE

Force Formulas - Static Friction, Kinetic Friction, Normal Force, Tension Force - Free Body Diagrams