DIFFERENTIATION | BEGINNER'S COURSE JEE 2025 / 2026 FULL PREP FROM BASICS | MATHEMATICALLY INCLINED
Neha Agrawal Mathematically Inclined・43 minutes read
The text focuses on the importance of understanding derivatives for JE exam preparation, covering topics such as average speed, differentiation rules, and the chain rule, emphasizing active participation and practice to enhance comprehension without memorization. It offers resources like hand-written notes, practice questions, and mock tests to support students in their learning journey, highlighting the value of quality education and free resources for exam preparation.
Insights
- Derivatives play a critical role in JE Mains and Advanced preparation, showcasing the significance of understanding concepts like average speed and instant speed, as well as the geometric and algebraic interpretations of derivatives.
- The text stresses the importance of actively engaging with differentiation rules, such as the chain rule, product rule, and logarithmic differentiation, emphasizing comprehension over rote memorization and encouraging consistent practice to master complex functions effectively.
Get key ideas from YouTube videos. It’s free
Recent questions
What is the importance of derivatives in JE Mains and Advanced preparation?
Derivatives are crucial for JE Mains and Advanced preparation, even if not explicitly mentioned in papers. They indicate the rate of change of one quantity concerning another, involving independent and dependent variables. Understanding derivatives helps in calculating average and instant speed, as well as finding the geometric meaning of tangents at specific points. Mastery of differentiation rules, like the chain rule and product rule, is essential for solving complex functions efficiently. Overall, a solid grasp of derivatives is fundamental for success in JE exams.
How are derivatives calculated for functions like e^x and sinx-cosx?
Derivatives of functions like e^x, sinx, and cosx involve specific rules and formulas. For e^x, the derivative remains e^x, emphasizing the importance of understanding constants in differentiation. When dealing with sinx and cosx, the derivative of sinx is cosx, and the derivative of cosx is -sinx. Applying differentiation rules correctly to these functions is crucial for accurate calculations and problem-solving in mathematics.
What is the process of finding higher-order derivatives?
Higher-order derivatives involve repeatedly differentiating a function. After finding the first derivative, the process continues by differentiating the result again to obtain the second derivative, and so on for subsequent orders. Each derivative provides information about the rate of change of the function at different levels, offering deeper insights into its behavior and characteristics. Understanding and calculating higher-order derivatives are essential skills in advanced mathematics and problem-solving.
How does logarithmic differentiation simplify finding derivatives?
Logarithmic differentiation simplifies finding derivatives by taking the logarithm of both sides of an equation. This technique allows complex functions to be transformed into simpler forms, making it easier to differentiate them using logarithmic properties. By applying logarithmic differentiation, intricate functions can be broken down into more manageable components, facilitating the process of finding derivatives accurately and efficiently.
Why is active participation and practice crucial for understanding differentiation concepts?
Active participation and practice are crucial for understanding differentiation concepts effectively. By engaging in learning sessions, quizzes, and practice problems, students reinforce their comprehension of differentiation rules and techniques. Regular practice helps solidify the understanding of derivative calculations, making it easier to apply them to various functions and problems. Active participation also fosters a deeper appreciation for the logic behind differentiation, moving beyond rote memorization to a more profound understanding of mathematical concepts.
Related videos

Science and Fun Education
Limits and Derivatives One Shot Maths | Class 11 Maths NCERT Explanation & Solution with Ushank Sir

Vora Classes
JEE Brief: Differential Equation Class 12 JEE One Shot Maths | JEE Main and Advanced | Nishant Vora

Arjuna JEE
Sets: COMPLETE Chapter in 1 Video | Quick Revision | Class 11 Arjuna JEE

Kalpit Veerwal
JEE 2026: Complete Guide to get AIR 1 (Books, Study Plan, Coaching) | Kalpit Veerwal
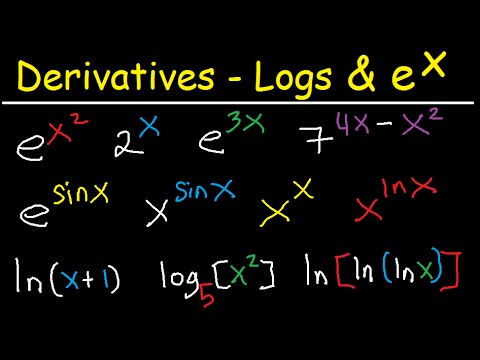
The Organic Chemistry Tutor
Derivatives of Exponential Functions & Logarithmic Differentiation Calculus lnx, e^2x, x^x, x^sinx
Summary
00:00
"Mastering Derivatives: Essential for Exam Success"
- The session is part of the 100 minutes daily dose beginner series, focusing on studying basics for students.
- The 21-day challenge covers 21 topics, with sessions lasting 70-75 minutes, followed by revision and solving DPP shared on the Tegra Group.
- Derivatives are crucial for JE Mains and Advanced preparation, even if not explicitly mentioned in papers.
- Average speed is calculated by dividing total distance by total time, but instant speed is more precise and relates to derivatives.
- Derivatives indicate the rate of change of one quantity with respect to another, involving independent and dependent variables.
- The derivative represents the change in one function concerning another, with notation like dy/dx for differentiation.
- The geometric meaning of derivatives involves tangents at points, showing the rate of change at specific instants.
- Differentiation rules include adding or subtracting derivatives, treating constants separately, and applying specific formulas for functions like e^x and sinx-cosx.
- Derivatives of functions like 3^x, e^x, and log(x) are explained, emphasizing the importance of understanding constants in differentiation.
- The session encourages active participation and understanding of differentiation concepts, reinforcing the importance of practice and comprehension.
20:51
Mastering Derivative Rules for Complex Functions
- When e and log are together, they cancel each other out, resulting in the derivative of a to the power of x.
- If a constant is present in the function, the derivative will be the constant multiplied by the original function.
- Patience is emphasized in waiting for the derivative to be calculated, with a reminder not to rush the process.
- The chain rule is compared to playing a game of Chain Chain, where each step builds upon the previous one.
- The derivative of sin2x is explained using a box in a box method, simplifying the process.
- The derivative of log x is shown to be 1/x, with a step-by-step explanation of the process.
- The product rule of differentiation is introduced, detailing how to differentiate functions that are multiplied together.
- The quotient rule is explained for functions that are divided, emphasizing the importance of the sequence of differentiation.
- Implicit functions are compared to making Khichdi, with the analogy used to explain the process of solving implicit functions.
- The importance of understanding and applying the rules of differentiation is highlighted for solving complex functions.
45:13
"Derivatives: Rules and Techniques for Finding"
- Differentiation process involves applying the product rule and chain rule to find derivatives.
- Implicit functions require differentiation by considering y as a separate variable.
- Explicit functions allow writing y in terms of x for differentiation.
- Chain rule is applied to find derivatives of functions involving x and y.
- Logarithmic differentiation simplifies finding derivatives by taking the logarithm of both sides.
- Higher-order derivatives involve repeatedly differentiating a function.
- Derivatives can be found by taking the derivative of the function with respect to a variable.
- The process of differentiation involves finding the derivative of a function with respect to a variable.
- Differentiation can be applied to functions involving multiple variables by considering each variable separately.
- The derivative of a function can be found by applying the product rule and chain rule as needed.
01:15:56
"Mastering Derivatives: JE Exam Prep Guide"
- The text discusses mathematical derivatives and the process of finding them quickly.
- It emphasizes the importance of understanding the logic behind derivative calculations rather than memorizing formulas.
- The text encourages active participation in quizzes and learning sessions to enhance understanding.
- It offers a comprehensive resource for JE exam preparation, including hand-written notes, practice questions, and mock tests.
- The text highlights the value of quality education and free resources in supporting students' learning and exam preparation efforts.




