17. Stochastic Processes II
MIT OpenCourseWare・33 minutes read
Continuous time stochastic processes, particularly Brownian motion, are complex but crucial in understanding various phenomena like stock prices and natural movements. Einstein's explanation of Brownian motion, along with Ito's calculus, highlights the significance and challenges of modeling such processes for financial and scientific purposes.
Insights
- Continuous time processes involve random variables indexed by real time, distinct from discrete processes with integer time values, posing challenges in describing their probability distribution due to the continuous nature of time intervals.
- Brownian motion, a continuous stochastic process named after Norbert Wiener, serves as a complex example with properties like normally distributed increments and independent increments for non-overlapping intervals, extending beyond theoretical observations to modeling physical quantities, including stock prices, and requiring specialized calculus like Ito's calculus to understand its behavior accurately.
Get key ideas from YouTube videos. It’s free
Recent questions
What is Brownian motion?
Brownian motion is a continuous stochastic process with normally distributed increments, starting at 0, and independent increments for non-overlapping intervals. It is defined by a probability distribution over continuous functions from positive reals to reals, describing its behavior over time.
Who discovered Brownian motion?
Brownian motion was discovered by Einstein in the context of observing pollen particles in water, exhibiting a random motion similar to Brownian motion in two dimensions.
How is Brownian motion used in finance?
Brownian motion can be used to model stock prices in finance due to continuous buying and selling actions affecting prices. It is also utilized in various fields, including finance and science, with Einstein's involvement highlighting its significance.
What is Ito's calculus?
Ito's calculus is motivated by the need to estimate infinitesimal differences in functions applied to Brownian motion, crucial in financial modeling. It involves understanding small-scale changes in Brownian motion and relating them to function differentiation.
What is the significance of Ito's lemma?
Ito's lemma states that df is equal to the first derivative term, dB_t, plus the second derivative term, double prime over 2 dt. This lemma enriches the theory of calculus when applied to Brownian motion, impacting the complexity and applicability of calculus involving Brownian motion.
Related videos

The Royal Institution
Chaos theory and geometry: can they predict our world? – with Tim Palmer

Wolfram
A conversation between Nassim Nicholas Taleb and Stephen Wolfram at the Wolfram Summer School 2021

TED
Benoit Mandelbrot: Fractals and the art of roughness
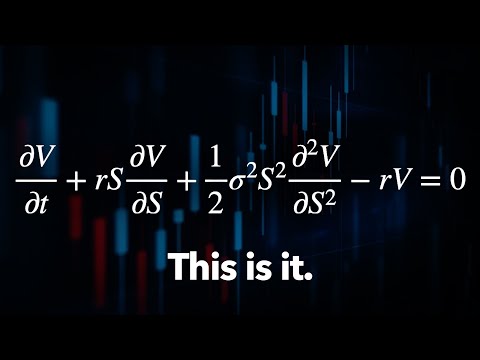
Veritasium
The Trillion Dollar Equation

Astrum
The 9 Experiments That Will Change Your View of Light (And Blow Your Mind)
Summary
00:00
Understanding Brownian Motion in Continuous Stochastic Processes
- Professor introduces the study of continuous types of stochastic processes after discussing discrete time processes, emphasizing the need to review concepts like variance, expectation, moments, moment generating function, Markov chains, and martingales.
- Continuous time processes involve random variables indexed by real time, unlike discrete time processes with integer time values.
- Describing the probability distribution of continuous time processes poses a challenge due to the continuous nature of time intervals.
- Brownian motion is introduced as a continuous stochastic process with specific properties: starting at 0, normally distributed increments, and independent increments for non-overlapping intervals.
- Brownian motion is defined by a probability distribution over continuous functions from positive reals to reals, with properties that describe its behavior over time.
- The complexity of continuous time processes is highlighted, with Brownian motion serving as a challenging example.
- Brownian motion is also known as Wiener process, named after MIT professor Norbert Wiener, and was initially studied for evaluating stock and auction prices.
- Brownian motion is described as the limit of simple random walks when time intervals are infinitely divided, connecting discrete observations to continuous processes.
- Brownian motion was discovered in the context of observing pollen particles in water, exhibiting a random motion similar to Brownian motion in two dimensions.
- The concept of Brownian motion extends beyond theoretical observations, with implications for modeling physical quantities and understanding natural phenomena like the movement of pollen particles in water.
20:58
Einstein's Brownian Motion: Finance and Science
- Einstein was the first to rigorously explain Brownian motion, linking it to simple random walks.
- Brownian motion is caused by tiny water molecules colliding with pollen particles, pushing them in random directions.
- Each collision between water molecules and pollen particles results in a small change in the particle's movement.
- Over time, these small changes accumulate, leading to a Brownian motion pattern.
- Stock prices can also be modeled using Brownian motion due to the continuous buying and selling actions affecting prices.
- Brownian motion is used in various fields, including finance and science, with Einstein's involvement highlighting its significance.
- Brownian motion properties include crossing the t-axis infinitely, not deviating significantly from a specific curve, and being nowhere differentiable.
- The non-differentiability of Brownian motion poses challenges for traditional calculus, leading to the development of Ito's calculus.
- The distribution of the minimum and maximum values of a stock price modeled by Brownian motion can be computed using specific formulas.
- The probability of the maximum value exceeding a certain threshold at a given time can be calculated using the properties of Brownian motion.
44:57
Understanding Brownian Motion and Ito's Calculus
- The distribution of the maximum value over a time interval is crucial in understanding Brownian motion.
- Brownian motion should always remain within a cone from time t to t+epsilon, based on its differentiability and slope.
- The maximum value over a time interval must be greater than epsilon times A to maintain control.
- The probability that the maximum value over a time interval is less than epsilon times A is related to the normal distribution of Brownian motion.
- The quadratic variation theorem for Brownian motion states that its variation does not diminish even with smaller scales, unlike differentiable functions.
- The quadratic variation for Brownian motion is significant theoretically and serves as a key lemma for Ito's calculus.
- The sum of squared differences in Brownian motion over intervals converges to T, showcasing its unique behavior.
- The percentile difference in stock prices following Brownian motion is a key concept in modeling financial derivatives.
- Ito's calculus is motivated by the need to estimate infinitesimal differences in functions applied to Brownian motion, crucial in financial modeling.
- While differentiating Brownian motion directly is not feasible, understanding its small-scale changes and relating them to function differentiation is a viable approach in Ito's calculus.
01:09:46
Ito's Lemma and dB_t squared: Crucial Concepts
- The formula dB squared equals dt arises from Taylor's expansion in calculus, where f of t plus x is expressed as f of t plus f prime of t times x, plus f double prime of t over 2 times x squared. In classical calculus, the difference between f(t+x) and f(t) was simplified to f prime t times x, but with Brownian motion, this simplification is no longer valid.
- Ito's lemma states that df is equal to the first derivative term, dB_t, plus the second derivative term, double prime over 2 dt. This lemma is highly respected and cited in research due to its nontrivial nature, as it enriches the theory of calculus when applied to Brownian motion.
- Remembering Ito's lemma and the concept that dB_t squared equals dt are crucial takeaways from the mathematical discussion, as they significantly impact the complexity and applicability of calculus involving Brownian motion.




