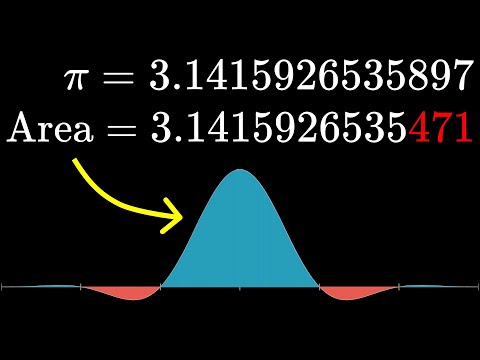
Euler's infinite pi formula generator
Mathologer・16 minutes read
The video explores Euler's mathematical leap leading to famous pi formulas through animated algebra and formulas. It delves into representing functions as infinite polynomials, Euler's crazy leap to derive a formula for sine, and manipulating his formula to derive infinite expressions for pi.
Insights
- Euler's groundbreaking work in the 18th century led to the development of famous pi formulas by representing functions like sine as infinite products based on their zeros, showcasing a unique approach to mathematical analysis and manipulation.
- Through meticulous manipulation of Euler's formulas, including logarithms and differentiation, subsequent mathematicians derived various infinite expressions for pi, such as the Leibniz-Madhava formula and Brouncker's infinite fraction formula, unveiling a systematic pattern of obtaining higher-order pi formulas by building upon Euler's original insights.
Get key ideas from YouTube videos. It’s free
Recent questions
What is the significance of Euler's leap in mathematics?
Euler's leap in mathematics, made in the 18th century, led to the discovery of key formulas for pi. This leap involved representing functions like sine as infinite products based on their zeros, resulting in famous infinite expressions for pi. By manipulating Euler's formula, mathematicians were able to derive formulas such as the Leibniz-Madhava formula and Brouncker's infinite fraction formula for pi. This mathematical breakthrough revolutionized the understanding of functions and paved the way for further developments in mathematical analysis.
How did Euler and his peers explore functions as infinite polynomials?
Euler and his peers explored functions as infinite polynomials by attempting to represent functions like sine as products based on their zeros. Euler's crazy leap to derive a formula for sine as an infinite product was a groundbreaking approach that challenged traditional mathematical thinking. By delving into the idea of functions as infinite polynomials, Euler and his peers were able to derive important formulas for pi and advance the field of mathematical analysis.
What inspired Euler's mathematical leap in the 18th century?
Euler's mathematical leap in the 18th century was inspired by the work of his peers and predecessors in the field of mathematics. Paul Levrie's article in the Mathematical Intelligencer in 2012 likely played a role in sparking Euler's curiosity and pushing him to explore new mathematical concepts. The collaborative nature of mathematical research during Euler's time contributed to the development of innovative ideas and breakthroughs in the field.
How did mathematicians derive the Leibniz-Madhava formula from Euler's product formula?
Mathematicians derived the Leibniz-Madhava formula from Euler's product formula by using techniques such as logarithms and differentiation. By manipulating Euler's formula and applying mathematical operations, they were able to extract the Leibniz-Madhava formula, which is a key expression in the realm of infinite series and pi calculations. This process of derivation showcases the intricate and interconnected nature of mathematical formulas and their relationships to one another.
What is the mystery behind the coefficients in the X to the power of five terms in the original expansion?
The coefficients of the X to the power of five terms in the original expansion are the mystery elements that mathematicians sought to uncover. By selecting the X in front and two x squared terms, with the rest being ones, mathematicians were able to manipulate the expanded product formula and derive various formulas for pi, including Euler's PI to the power of 6 formula. The mystery behind these coefficients lies in their role in the overall mathematical manipulation process and their significance in deriving complex mathematical expressions.
Related videos
Summary
00:00
Euler's Mathematical Leap to Pi Formulas
- Mathologer video revisiting a mathematical leap by Leonhard Euler in the 18th century.
- Euler's leap resulted in a key leading to famous pi formulas.
- Demonstrating the leap with animated algebra for Leibniz-Madhava, Wallis, Brouncker, and Euler's formulas for pi.
- Inspired by Paul Levrie's article in the Mathematical Intelligencer in 2012.
- Exploring the idea of functions as infinite polynomials by Euler and his peers.
- Euler's attempt to represent functions like sine as products based on their zeros.
- Euler's crazy leap to derive a formula for sine as an infinite product.
- The process of manipulating Euler's formula to derive famous infinite expressions for pi.
- Deriving Leibniz-Madhava formula from Euler's product formula using logarithms and differentiation.
- Manipulating Euler's formula to derive Brouncker's infinite fraction formula for pi.
22:30
"Unveiling Mysteries: Coefficients and Euler's Formulas"
- The coefficients of the X to the power of five terms in the original expansion are the mystery stuff in the bracket, obtained by selecting the X in front and two x squared terms, with the rest being ones.
- The sum of the reciprocals of the fourth powers of integers is the desired outcome, achieved by replacing the less than sign with an equal sign in the sum of all coefficients.
- By manipulating the expanded product formula and deriving Euler's PI to the power of 6 formula, a series of formulas including PI to the power of 8 can be obtained, following a consistent manipulation pattern.